Vanilla Encoding
Vanilla Encoding example
여기서는 $z \in \mathbb{C}^N$를 다항식 $m(X) \in \mathbb{C}[X]/(X^N + 1)$로 encoding하는 간단한 경우를 다룰 것입니다.
이를 위해 $\sigma: \mathbb{C}[X]/(X^N + 1) \rightarrow \mathbb{C}^N$이라는 canonical embedding을 사용할 것인데, 이는 벡터를 decoding하고 encoding합니다.
다항식 $m(X)$을 vector $z$로 decoding하려면 이 다항식을 특정 값에서 평가해야 하는데, 이 값은 cyclotomic polynomial $\Phi_M(X) = X^N + 1$의 root일 것입니다. 이 $N$개의 root는 $\xi, \xi^3, …, \xi^{2N-1}$입니다.
따라서 다항식 $m(X)$을 decoding하려면 $\sigma(m) = (m(\xi), m(\xi^3), …, m(\xi^{2N-1})) \in \mathbb{C}^N$으로 정의합니다. $\sigma$는 isomorphism을 정의하는데, 이는 bijective homomorphism으로, 따라서 어떤 벡터든지 해당하는 다항식으로 고유하게 encoding되고 그 반대도 성립합니다.
여기서 $\sigma$는 decoding이므로, 역함수 $\sigma^{-1}$을 계산하는 것은 vector $z \in \mathbb{C}^N$를 해당 다항식으로 encoding하는 것이 됩니다. 따라서 문제는 vector $z \in \mathbb{C}^N$가 주어졌을 때 다항식 $m(X) = \sum_{i=0}^{N-1} \alpha_i X^i \in \mathbb{C}[X]/(X^N + 1)$을 찾는 것인데, 이 때 $\sigma(m) = (m(\xi), m(\xi^3), …, m(\xi^{2N-1})) = (z_1, …, z_N)$가 됩니다.
이를 더 깊게 파헤치면 다음과 같은 시스템이 나옵니다:
$\sum_{j=0}^{N-1} \alpha_j (\xi^{2i-1})^j = z_i, \quad i=1, …, N.$
이는 다음과 같은 선형 방정식으로 볼 수 있습니다:
$A \alpha = z$
여기서 $A$는 $(\xi^{2i-1})_{i=1}^{N}$의 Vandermonde 행렬이고, $\alpha$는 다항식 계수의 벡터이며, $z$는 encoding하려는 벡터입니다.
따라서 $\alpha = A^{-1}z$이고, $\sigma^{-1}(z) = \sum_{i=0}^{N-1} \alpha_i X^i \in \mathbb{C}[X]/(X^N + 1)$임을 알 수 있습니다.
여기서 $M=8$, $N=\frac{M}{2}=4$, $\Phi_M(X)=X^4+1$, 그리고 $\omega=e^{\frac{2i\pi}{8}}=e^{\frac{i\pi}{4}}$로 두겠습니다. 목표는 다음 벡터들을 encoding하고 decoding한 후, 그 다항식을 더하고 곱한 다음 이를 다시 decoding하는 것입니다: $[1, 2, 3, 4]$ 및 $[-1, -2, -3, -4]$.
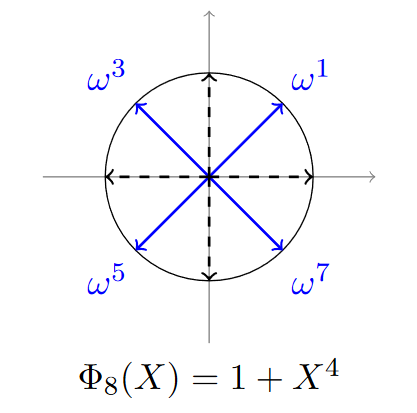
다항식을 decoding하기 위해서는 단순히 power of an $M$-th root of unity에서 평가하면 됩니다. 여기서는 $\xi_M = \omega = e^{i\pi/4}$를 선택합니다.
$\xi$와 $M$이 주어지면 $\sigma$ 및 그 역함수 $\sigma^{-1}$을 정의할 수 있습니다. 각각 decoding과 encoding을 나타냅니다.
import numpy as np
from numpy.polynomial import Polynomial
np.set_printoptions(precision=3) # 소수점 3자리만 출력하도록 setting
Vanilla Encoder Class 선언
class CKKSEncoder:
"""Basic CKKS encoder to encode complex vectors into polynomials."""
def __init__(self, M: int):
"""
Initialization of the encoder for M a power of 2.
xi, which is an M-th root of unity will, be used as a basis for our computations.
"""
# ========================= EDIT HERE =========================
self.xi = np.exp(2 * np.pi * 1j / M)
# =============================================================
self.M = M
@staticmethod
def vandermonde(xi: np.complex128, M: int) -> np.array:
"""Computes the Vandermonde matrix from a m-th root of unity."""
N = M // 2
matrix = []
# We will generate each row of the matrix
for i in range(N):
# For each row we select a different root
# ========================= EDIT HERE =========================
root = xi ** (2 * i + 1)
# =============================================================
row = []
# Then we store its powers
for j in range(N):
# ========================= EDIT HERE =========================
row.append(root ** j)
# =============================================================
matrix.append(row)
return matrix
def sigma_inverse(self, b: np.array) -> 'Polynomial':
"""Encodes the vector b in a polynomial using an M-th root of unity."""
# First we create the Vandermonde matrix
A = CKKSEncoder.vandermonde(self.xi, self.M)
# Then we solve the system
"""
선형 방정식 Mx = y의 해는 np.linalg.solve(M, y)로 구할 수 있습니다.
"""
# ========================= EDIT HERE =========================
coeffs = np.linalg.solve(A, b)
# =============================================================
# Finally we output the polynomial
p = Polynomial(coeffs)
return p
def sigma(self, p: Polynomial) -> np.array:
"""Decodes a polynomial by applying it to the M-th roots of unity."""
outputs = []
N = self.M //2
# We simply apply the polynomial on the roots
for i in range(N):
# ========================= EDIT HERE =========================
root = self.xi ** (2 * i + 1)
# =============================================================
output = p(root)
outputs.append(output)
return np.array(outputs)
# Set the parameters
M = 8
# Initialize our encoder
encoder = CKKSEncoder(M)
Vandermonde matrix란?
"""What is Vandermonde matrix?"""
matrix = encoder.vandermonde(encoder.xi, encoder.M)
print(np.array(matrix))
[[ 1. +0.j 0.707+0.707j 0. +1.j -0.707+0.707j]
[ 1. +0.j -0.707+0.707j 0. -1.j 0.707+0.707j]
[ 1. +0.j -0.707-0.707j 0. +1.j 0.707-0.707j]
[ 1. +0.j 0.707-0.707j 0. -1.j -0.707-0.707j]]
Polynomial로 Encoding
b = np.array([1, 2, 3, 4])
p = encoder.sigma_inverse(b)
Polynomial(p.coef.round(3))
$ x ↦ (2.5+0j)+((-0+0.707j))x+((-0+0.5j))x^2+(0.707j)x^3 $
Decoding
b_reconstructed = encoder.sigma(p)
b_reconstructed
array([1.+1.110e-16j, 2.+1.110e-16j, 3.+5.551e-17j, 4.-2.220e-16j])$
Error
np.linalg.norm(b_reconstructed - b)
$2.7755575615628914e-16$
Addition
m1 = np.array([1, 2, 3, 4])
m2 = np.array([1, -2, 3, -4])
p1 = encoder.sigma_inverse(m1)
p2 = encoder.sigma_inverse(m2)
Polynomial(p1.coef.round(3))
$x ↦ (2.5+0j) + ((-0+0.707j))x + ((-0+0.5j))x^2 + (0.707j)x^3$
Polynomial(p2.coef.round(3))
$x ↦ (-0.5+0j)+((-0.707+0j))x+(-2.5j)x^2+((0.707+0j))x^3$
p_add = p1 + p2
Polynomial(p_add.coef.round(3))
$x ↦ (2+0j)+((-0.707+0.707j))x+((-0-2j))x^2+((0.707+0.707j))x^3$
Decoding 결과
encoder.sigma(p_add)
array([ 2.000e+00-9.197e-17j, -8.882e-16+2.220e-16j,
6.000e+00+2.220e-16j, -4.441e-16+0.000e+00j])
Multiplication
poly_modulo = Polynomial([1, 0, 0, 0, 1])
poly_modulo
$x ↦ 1.0+0.0x+0.0x^2+0.0x^3+1.0x^4$
p_mult = p1 * p2
Polynomial(p_mult.coef.round(3))
$x↦(-1.25+0j)+((-1.768-0.354j))x+(-7j)x^2+((3.536-0.707j))x^3+((1.25+0j))x^4 +((1.768+0.354j))x^5+(0.5j)x^6$
이렇게 4차 함수를 넘어가기 때문에 위 다항식인 $x^4+1$(Cyclotomic polynomial)으로 나눠주어야 한다.
p_mult = p1 * p2 % poly_modulo
Polynomial(p_mult.coef.round(3))
$ x↦(-2.5+0j)+((-3.536-0.707j))x+((-0-7.5j))x^2+((3.536-0.707j))x^3$
Decoding 결과
encoder.sigma(p_mult)
array([ 1.+7.216e-16j, -4.+8.327e-16j, 9.-5.274e-15j, -16.-2.609e-15j])
Reference
https://blog.openmined.org/ckks-explained-part-1-simple-encoding-and-decoding/


